Lugar geométrico III

He aquí un nuevo problema

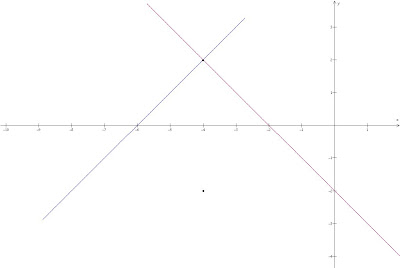
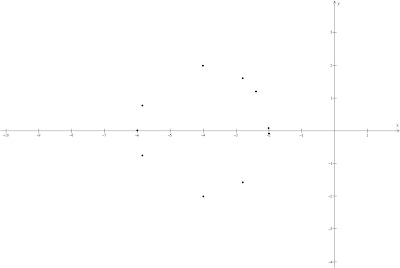
Obtener la ecuación del lugar geométrico del punto P(x,y) tal que las longitudes de las lineas tangentes de P a cada uno del siguiente par de circunferencias sea igual.
$$x^2+y^2=3$$
$$(x+2)^2+(y-2)^2=2$$

Respuesta al problema de la Lugar geométrico

Aquí está la respuesta al segundo problema del lugar geométrico
 Primero veremos que pasa gráficamente.
Cuando $$m=1$$

 Con $$m=-1$$

Muchos puntos después

y wow! al parecer nos ha quedado una bonita circunferencia con centro en (-4,0) y radio 2

Escribiendo las ecuaciones de nuevo
$$m x-y+2m=0$$ ...(1)
$$x + m y + 6 = 0$$  ...(2)
De la ecuación 1
$$m(x+2)-y=0$$
Despejando m
$$m=\frac{y}{x+2}$$ (3)
Con la ecuación 3 tenemos 2 posibles casos.
Caso I $$x\neq -2$$
Sustituyendo (3) en (2) y simplificando
$$x+\frac{y^2}{x+2}+6=0$$
$$x^2+2x+y^2+6x+12=0$$
$$x^2+8x+y^2+12=0$$
Completando T. C. P.
$$x^2+8x+16+y^2=16-12$$
$$(x+4)^2+y^2=4$$ (4)
Como lo decía la gráfica, tenemos una circunferencia con centro en (-4,0) y radio 2
Ahora veamos
Caso II $$x=-2$$
de (1) $$y=0$$
Pero esto no satisface (2) ya que $$-2+m(0)+6=4\neq 0$$
Entonces de los casos I y II
Queda que la ecuación del lugar geométrico es una circunferencia con centro en (-4,0) y radio 2 (Ecuación (4)) exceptuando el punto (-2,0)

Respuesta del problema de la semana

Por fin la tan esperada respuesta del problema de la semana. Después de tanto pensar, he aquí la respuesta:

Escencialemte hay dos casos distintos: cuando uno de los dígitos pares repetido está al final del número (cuando se lee el número de izquiera a derecha); y cuando los dígitos iguales están en las primeras cuatro posiciones.
En el primer caso, cuando el dígito par repetido está al final del número, entonces el otro dígito igual debe estar en la primera, segunda o tercera posición, es decir tenemos 3 posiciones y 5 posibles números pares. En cualquiera de estos casos tenemos que escoger una posición para el impar, lo cual podemos hacer de tres maneras, y tenemos 5 posibles números impares. Una vez hecho esto, debemos colocar dos pares en las dos casillas restantes. Para el primer par tenemos cuatro posibilidades, pues ya pusimos el par que se repite y para el segundo par tenemos sólo 3 posibilidades. Por lo tanto en este caso hay
3.5.3.5.4.3=2700 casos

En el segundo caso, el par repetido puede ir en las casillas, una y tres, una y cuatro, dos y cuatro. Es decir tres casos, con 5 números posibles para este par. En la casilla final debe ir un par, para el cual tenemos 4 posibles pares. Quedan dos casillas libres. Una de las cuales es para el impar, es decir tenemos 2 posibilidades para poner cualesquiera de los 5 impares; y para el último tenemos 3 números posibles. En total hay 3.5.4.2.5.3=1800. Luego la respuesta final es 2700 + 1800 = 4500

ŞξŖĞεαŊ∏ Ρ€рР℮® encontró la respuesta correcta :D

Problema de la semana

Después de mucho pensar, he optado por publicar un pequeño problema que no dudo que todos podrán resolver.


Una banda de ladrones quiere encontrar la combinación de la caja fuerte de un banco y tiene la siguiente información: la combinación consiste en 5 dígitos y es un número par; exactamente uno de los 5 dígitos es impar; la combinación tiene 4 dígitos diferentes, el dígito repetido es par y aparece en posiciones no consecutivas. ¿Cuántas combinaciones deben intentar los ladrones?

Lugar geométrico

En vista del exito obtenido con el último problema, aqui va otro que espero tenga alguna respuesta

Dadas las 2 rectas $$m x-y+2m=0$$ ...(1) y $$x + m y + 6 = 0$$ ...(2)
Obtener la ecuación del lugar geométrico de los puntos de intersección $$\forall m\in \mathbb{R}$$

Respuesta al problema de la elipse

Como nadie pudo resolver el problema de la elipse entonces escribiré la respuesta.
Empezamos con dibujar la elipse

Como ya sabemos la elipse tiene 2 rectas tangentes con una misma pendiente y también dibujamos sus rectas perpendiculares.

Ahora dibujamos otro grupo de tangentes perpendiculares

Marcando los puntos de intersección obtenidos

Al parecer hemos obtenido una circunferencia

Ahora veremos que dicen las ecuaciones
Ya teniamos que las ecuaciones de las rectas tangentes a la elipse son $$y=\text{mx}\pm \sqrt{a^2m^2+b^2}$$ (1)
Para que tengamos una recta perpendicular necesitamos que tenga pendiente $$-\frac{1}{m}$$
Entonces su ecuación es $$y=-\frac{1}{m}x\pm \sqrt{\frac{a^2}{m^2}+b^2}$$
Acomodando nos queda $$y=\frac{-x\pm \sqrt{a^2+m^2b^2}}{m}$$ (2)
De (1) y de (2)
$$y-\text{mx}=\pm \sqrt{a^2 m^2+b^2}$$ (3)
$$\text{my}+x=\pm \sqrt{a^2+m^2b^2}$$ (4)
Elevando (3) y (4) al cuadrado
$$y^2-2\text{mxy}+m^2x^2=a^2 m^2+b^2$$ (5)
$$m^2y^2+2\text{mxy}+x^2=a^2+m^2b^2$$ (6)
Sumando (5) y (6)
$$y^2+m^2x^2+m^2y^2+x^2=a^2 m^2+b^2+a^2+m^2b^2$$ (7)
Factorizando
$$x^2\left(m^2+1\right)+y^2\left(m^2+1\right)=a^2\left(m^2+1\right)+b^2\left(m^2+1\right)$$
$$\left(m^2+1\right)\left(x^2+y^2\right)=\left(m^2+1\right)\left(a^2+b^2\right)$$
Como $$m^2+1\neq 0$$
$$x^2+y^2=a^2+b^2$$ (8)
Lo que dá una circunferencia con radio $$\sqrt{a^2+b^2}$$
A (8) se le llama círculo director

Leonhard Euler

Leonhard Euler fue un matématico y físico. Nació en Basilea (Suiza) el 15 de Abril de 1707 (así que hoy cumple 303 años) y murió el 18 de Septiembre de 1783 en San Petesburgo (Rusia). Euler  es considerado como el matemático más prolífico de la historia.

El padre de Leonhard dejaba que tomara una vez a la semana clases de matemáticas con otro matemático de Basilea llamado Johann Bernoulli. A los 16 años recibirió el título de maestro de Filosofía

Leonhard  trabajó en  geometría, cálculo, trigonometría, álgebra, teoría de números, además de física continua, teoría lunar y otras áreas de la física. Euler introdujo el término de función y fue el primero en usar f(x).
Introdujo la notación de las funciones trigonométricas,  el simbolo $$\sum$$ para representar sumas, uso $$e$$ para representar la base de los logaritmos naturales, uso la $$i$$ como la unidad imaginaria y popularizo el uso de la letra $$\pi$$ para representar el cociente entre la circunferencia y su diámetro

A sus 28 años Euler resolvió el problema de Basilea en el cuál habian fallado los grandes matemáticos de la época. El problema consistia en hallar el valor de $$\sum _{n=1}^{\infty } \frac{1}{n^2}$$ el cuál resultó ser $$\frac{\pi ^2}{6}$$

Descubrió la llamada fórmula de Euler $$e^{i \alpha }=\text{Cos}[\alpha ]+i \text{Sen}[\alpha ]$$
Donde se obtiene que $$e^{i \pi }+1=0$$

En geometría descubrió el baricentro, circuncentro y ortocentro además descubrió que los 3 puntos se hallaban en la misma recta,  la que se conoce como recta de Euler.

Encontró que en un grafo conexo $$\text{Vertices}-\text{Aristas}+\text{Caras}=2$$

Integró el cálculo diferencial de Leibniz con el Método de Fluxión de Newton, y desarrolló herramientas que hacían más fácil la aplicación del cálculo a los problemas físicos.

Euler  introdujo explícitamente los conceptos de partícula y de masa puntual y la notación vectorial para representar la velocidad y la aceleración. Empezó a trabajar en electromagnetismo 100 años antes de Maxwell.

Bueno si continuo con sus descubrimientos este artículo se hara enormemente largo asi que solo será hasta aquí.

Pierre Simon Laplace decía

Leed a Euler, leed a Euler. Él es el maestro de todos nosotros

Elipse

Aqui les dejo un problema de geometría analítica
Hallar la ecuación del lugar geométrico del punto de intersección de dos rectas perpendiculares cualesquiera tangentes ambas a la elipse.
$$b^2x^2+a^2y^2=a^2b^2$$

Sugerencia. Primero encuentra las ecuaciones de las rectas tangentes con pendiente $$m$$

Ayudaré con la sugerencia.

La garra del león (Parte 2)

El primero de los problemas propuesto por Bernoulli era determinar la braquistócrona (del griego brachistos, el más breve, y cronos, tiempo), lo que significa que trayectoria debe seguir un cuerpo que se mueve unicamente por la fuerza gravitatoria para que recorra la distancia de un punto A a un punto B en el menor tiempo posible. La respuesta es la cicloide.

Ahora encontraremos la ecuación de una cicloide

En la figura se observa el círculo que gira sobre la linea horizontal. Sea el punto $$P (x,y)$$ un punto arbitrario de la cicloide, $$C$$ es el centro de la circunferencia. Se traza una linea paralela al eje desde $$P $$ hasta $$D$$ y se marcan los puntos $$A$$ y $$B$$ que son los puntos $$P$$ y $$D$$ proyectados en el eje. $$a$$ es el radio de la circunferencia que genera la cicloide y $$\theta$$ es el ángulo que ha girado la circunferencia. 

Como la circunferencia gira desde el origen $$0$$ hasta $$B$$, 

$$\overline{\text{OB}}=\text{Arco} \overline{\text{PB}}$$

$$\text{Arco} \overline{\text{PB}}=\text{a$\theta $}$$

De la figura

$$x= \overline{\text{OA}}= \overline{\text{OB}}- \overline{\text{AB}}=\overline{\text{OB}}- \overline{\text{PD}}=\text{a$\theta $}-a \text{Sen}[\theta ]$$

$$y= \overline{\text{AP}}= \overline{\text{BD}}= \overline{\text{BC}}- \overline{\text{CD}}=a-a \text{Cos}[\theta ]$$

Esta es la ecuación paramétrica de la cicloide. donde cada $$2\pi$$ se genera un bucle. 

De la segunda ecuación.

$$\text{Cos}[\theta ]=\frac{a-y}{a}$$

$$\theta =\text{ArcCos}\left[\frac{a-y}{a}\right]$$

$$\text{Sen}[\theta ]=\sqrt{1-\text{Cos}^2[\theta ]}=\frac{\sqrt{2\text{ay}-y^2}}{a}$$

Sustituyendo en la primera ecuación

$$x=a \text{ArcCos}\left[\frac{a-y}{a}\right]-\sqrt{2\text{ay}-y^2}$$

Esta ecuación solo da la primera mitad de la cicloide. para graficar la segunda mitad se usa

$$x=2\pi -\left(a \text{ArcCos}\left[\frac{a-y}{a}\right]-\sqrt{2\text{ay}-y^2}\right)$$

 A continuación dejo unos videos de la braquistócrona y de la Tautócrona (que resulta también ser la cicloide) qué es cuando dos partículas soltadas en cualquier punto de la cicloide llegaran al punto central en el mismo tiempo.

La garra del león (Parte 1)

Una cicloide es el lugar geométrico descrito por cualquier punto fijo de una circunferencia que rueda, sin resbalar, sobre una recta fija. Galileo Galilei le dio el nombre de cicloide en 1599.

En 1696 Johann Bernoulli presentó a la comunidad científica 2 problemas. Al que lograra resolver los dos problemas en un plazo de 6 meses le regalaría un libro de su biblioteca personal (el cuál en esa época era demasiado caro). Al pasar los 6 meses el único que presentó una solución fue Leibniz pero solo pudo resolver el primer problema. Como el trato era resolver los dos problemas Johann puso otros 6 meses de plazo, al pasar el año aparte de Leibniz otros 4 habian logrado resolver el primer problema: Guillaume de l'Hôpital, Tschirnhaus, Johann Bernoulli y Jacob Bernoulli.

Entonces al ver los resultados Leibniz le propuso a Johann que le presentaran los problemas a Isaac Newton. Johann muy contentó aceptó la petición de Leibniz (ya que Bernoulli apoyaba a Leibniz en la invención del cálculo, y esta era una buena forma de burlarse de Newton cuando no pudiera resolver los problemas). Asi que Johann mandó a Edmond Halley a la casa de Newton a entregarle una carta en la cuál explica los problemas y agrega que muy pocas personas pueden resolver los problemas formulados por Johann (sin duda se quiere burlar de él).

El 29 de enero de 1697 Halley llegó a casa de Newton. Halley recuerda

Llegué a su casa a las dos de la tarde. Él estaba encerrado en su estudio, y la servidumbre tenía estrictas órdenes de no molestarlo ni abrir la puerta por ningún motivo. Por lo tanto, me senté afuera a esperar que saliera. Rato después, el ama de llaves trajo el almuerzo de Newton en una bandeja, y lo dejó en el piso, frente a la puerta. Las horas pasaron. A las seis de la tarde, yo sentía un hambre atroz, y me atreví a devorar el pollo de la bandeja. Cuando Newton por fin abrió la puerta, miró los huesos del pollo en la bandeja, me miró a mí y exclamó: —¡Qué distraído soy! ¡Pensé que no había comido!

Entonces Halley le explicó la situación entregandole la carta y Newton dijo "luego le echo una ojeada a los problemas". A las 4 de la mañana del dia siguiente Newton había resuelto los 2 problemas (en menos de 10 horas) y a las 8 mando una carta a la Royal Society con su solución pero sin poner firma. Los desarrollos de Newton fueron publicados en febrero como forma anónima. Cuando Bernoulli vio la elegancia de sus soluciones dijo "Es Newton", cuando le preguntaron "¿Cómo lo sabe?" solo respondió "Ex ungue leonis", figuradamente "Porque reconozco las garras del león" o "Por sus garras se conoce al león", en el sentido de que el estilo claro, conciso, brillante y definitivo de Newton era fácilmente reconocible para él.

Problema

Como mi primer post (sin contar el de bienvenida) hoy les voy a dejar un pequeño problema sobre trigonometria.

Calcular el valor del siguiente producto

$$\frac{\text{Sen} 1{}^{\circ}}{\text{Cos} 1{}^{\circ}}\cdot \frac{\text{Sen} 2{}^{\circ}}{\text{Cos} 2{}^{\circ}}\cdot \text{...}\cdot \frac{\text{Sen} 88{}^{\circ}}{\text{Cos} 88{}^{\circ}}\cdot \frac{\text{Sen} 89{}^{\circ}}{\text{Cos} 89{}^{\circ}}$$

BIENVENUS MES AMIS

Bienvenidos de nuevo a este nuevo blog, que esperamos sea de su completo agrado. Creado especialmente para difundir la Física y las Matemáticas. ¿Por qué no empezar por un problema fácil para dar comienzo a este blog?

Los empleos de Juan, Marco y Raúl son panadero, taxista y bombero. A Marco y a Raúl les gusta el beisbol y al taxista no. El panadero colecciona timbres. Raúl no sabe nada de sellos certificados. ¿Quién es panadero?

A Marco y a Raúl les gusta el beisbol, y al taxista no. Lo que implica que Juan es el taxista.
Raúl no sabe nada de certificados, lo que implica que él no colecciona timbres dado a que si lo hiciera, sabria de sellos certificados.
Por lo que Marco es el panadero y Raúl es el bombero.

Esto demuestra que las matemáticas no son sólo fórmulas matemáticas o gráficas en una hoja milimétrica o un ordenador. Y bienvenidos de nuevo.

Bienvenidos

Este blog está pensado para escribir artículos sobre Física y Matemáticas (tal vez algunas otras cosas). Espero que les guste y comenten.

$$\sum _{n=1}^{\infty } n$$

Si no pueden ver la imagen anterior les recomiendo que utilicen Mozilla Firefox (o cualquiera que no sea Internet Explorer) para poder visualizar las fórmulas en LaTex